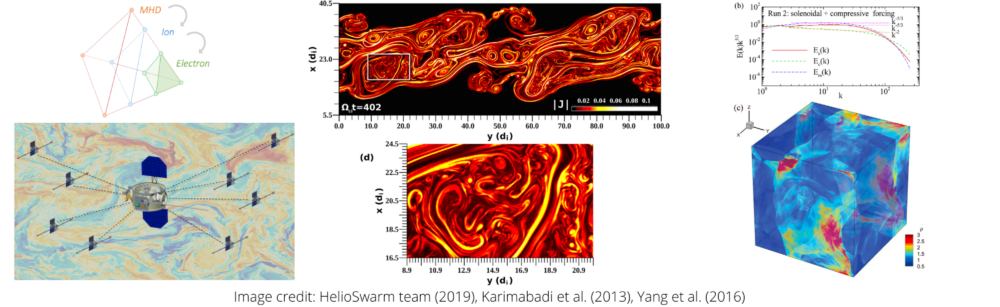
Plasmas constitute the most significant proportion of visible matter in the Universe. Nevertheless, how energy is transferred from large to small scales, between its different forms, and eventually dissipated in plasmas remains an open question. Specifically, how do plasma processes dissipate the energy stored in magnetic fields and thereby cause the energy transfer that heats surrounding environments to extreme temperatures? For example, the solar corona reaches over 1 million Kelvin (e.g., Klimchuk, 2006) and the intergalactic medium over 10 million Kelvin (e.g., Bykov et al., 2008). A second, equally important question concerns how physical processes (e.g., in the solar wind and supernova remnants) energize charged particles to very high energies. Space and astrophysical plasmas ubiquitously exhibit strong, broadband turbulent fluctuations. These turbulent fluctuations nonlinearly interact, allowing the cross-scale energy transfer from very large energy-containing to smaller scales as shown in Fig 1, resulting in plasma heating and particle energization. Turbulent plasmas in the solar-terrestrial environments offer a unique, natural laboratory where fundamental processes at work can be probed in situ.
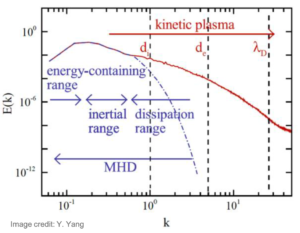
To answer how plasmas transfer and dissipate energy, we need to understand the energy conversion between different forms and the energy transfer across scales. Energy in plasmas can be categorized as electromagnetic, fluid flow, and thermal energies. The energy conversion and transfer are facilitated by dynamical mechanisms, which may operate differently depending on the environment and local forcing. A number of works have considered energy conversion and transfer via physical processes such as magnetic reconnection (e.g., Birn & Hesse, 2010; Fadanelli et al., 2021; Guo et al., 2021; Pucci et al., 2018; Stawarz et al., 2022; 2021), shocks (e.g., Schwartz et al., 2021), turbulence (e.g., Yang, 2019), instabilities (e.g., Maruca et al., 2011), and wave-particle interaction (Klein et al., 2020; Narita & Marsch, 2015). The energy conversion is done via two main channels: from the electromagnetic energy into the kinetic (fluid flow and thermal) and from the flow into thermal energy. Meanwhile, the energy is also transferred from large (MHD) scales to small (kinetic) scales of ions and electrons (Fig 1). Crucially, how the energy is finally dissipated into heat at the smallest scale in different situations is still under considerable debate. With the new generation of space missions and the kinetic 3-D simulations, we have more tools to progress towards a closure of the problem. Nevertheless, several challenges need to be overcome. Our proposed ISSI team focuses on the two main issues.
(1) Various formulations of the energy transfer problems
There exist a number of formulations to estimate energy transfer rates based on certain assumptions. This fact hinders direct comparisons to investigate the relative importance of disparate processes in different situations. For the theoretical description of plasmas, the Liouville equation of many-body distribution functions is the complete statistical description. However, the information contained in the many-body distribution function is too vast to ever be measured, analyzed, or simulated. Instead, we must rely on a series of models, each of which is based on a unique set of approximations that are valid across a sub-range of spatial and temporal scales. At energy-containing scales (see Fig 1), for example, a von Karman-Howarth picture (Kármán, 1938) of turbulent decay was extended for MHD (Hossain, et al. 1995; Wan, et al., 2012), in which the global decay rate of energy is controlled by the von Karman decay law. Laws governing the behavior of statistical third-order structure functions in the inertial range, i.e., Politano-Pouquet law (Politano and Pouquet, 1998), are among the few rigorous results in homogeneous, isotropic MHD turbulence. This law has been widely used in estimating the heating rate of solar wind in the past 20 years (e.g., Marino et al., 2008). Despite the multiplicity of energy transfer (or dissipation) rate proxies, their validity relies on assumptions. For example, a major issue in the application of the Politano-Pouquet law in the solar wind is assuming isotropy in turbulence that is actually anisotropic for solar wind (e.g., Horbury et al., 2012).
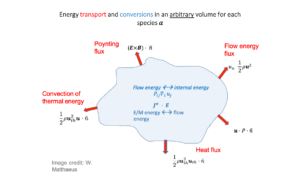
To estimate the energy transfer between forms, one direct way is to consider the governing equations of mass, momentum, and energy conservation laws for an ensemble of plasma species using the Boltzmann equation (i.e., kinetic description) and with the Vlasov-Maxwell limit (e.g., Birn & Hesse, 2010; Fadanelli et al., 2021; Yang et al., 2017). This approach leads to a description, illustrated as a cartoon in Fig 2, of the energy transport terms (red) and conversion terms (blue) in an arbitrary volume for each plasma species. Kinetic Particle-In-Cell (PIC) simulations provide a direct tool to study those terms. More recently, thanks to the four-spacecraft tetrahedral formation and the high-resolution observations of particle velocity distributions by MMS, such terms have been investigated in situ (e.g., Bandyopadhyay et al., 2021; Stawarz et al., 2017; 2021b). However, due to limited point and single-scale observations, a careful analysis is critically needed.
1st Scientific Goal Our team seeks to compare and synthesize different formulations and provide feasible and reasonable ways to measure energy transfer or dissipation rate that could be applied to in situ observations (e.g., MMS, Cluster, HS, Parker Solar Probe, and Solar Orbiter). The review of the energy transfer formulations and employed assumptions will facilitate discussions of the relative importance of different mechanisms, as well as identify gaps that may be addressed by future studies.
(2) Multi-point analyses of energy transfer and associated mechanisms
Understanding of energy transfer in turbulent plasmas has been significantly advanced thanks to in situ measurements from missions such as MMS. However, due to limited observation points, we cannot directly evaluate energy exchanges, which require the consideration of a plasma volume (Fig 2), nor accurately deduce the multi-scale properties of turbulent fluctuations. Using single-spacecraft measurements, the assumption that the temporal measurements are equivalent to the spatial variations (Taylor, 1938) is typically employed. However, Taylor’s assumption is not always valid, especially at electron scales where the energy eventually dissipates (e.g., Perri et al., 2017). The four-spacecraft tetrahedra – Cluster and MMS – have been game changers because they allow direct examination of plasma structures in 3-D via linear-gradient estimations (e.g., Chanteur & Harvey, 1998; Shen et al., 2003), including terms in Fig 2. Nevertheless, errors from the estimation, which are of the second order, have largely been ignored. Also, the study of energy exchanges at the boundary of a plasma volume has been limited. We aim to address these limitations by revisiting multi-spacecraft techniques and the employed assumptions for estimating energy transfer rates with in situ data. We will also identify associated mechanisms responsible for energy transfer in various conditions by exploiting data from MMS, Cluster, and other missions.
Testing multi-spacecraft analysis techniques has been proven to be a valuable approach for interpreting results from in situ observations as well as understanding their limitations (e.g., Kieokaew et al., 2018). We will employ virtual probes in 3-D kinetic and MHD simulations of turbulent plasmas (e.g., Pucci et al., 2017; Yang et al., 2016) and compare the results with in situ data. With lessons learned from 4-spacecraft missions, we may also test tools with larger constellations, e.g., the nonlinear gradient estimations with 10 spacecraft (Shen, et al., 2021) and magnetic field reconstruction with 24 spacecraft (Maruca et al., 2021). Nine-spacecraft HS, for example, will provide cross-scale polyhedral formation in which several techniques could be tested (e.g., Broeren et al., 2021; Klein et al., 2019; Matthaeus et al., 2019).
2nd Scientific Goal We propose a synergy between 3-D numerical simulations (kinetic and MHD) and multi-spacecraft applications to investigate the energy transfer measures and associated mechanisms. Particular emphasis will be placed on the exploitation of multi-spacecraft tools in order to discuss the advantages and disadvantages of existing tools and identify future developments with a larger number of spacecraft.
Reference
Bandyopadhyay, R., et al. “Energy Dissipation in Turbulent Reconnection”, Physics of Plasmas, no. 2, 2021, doi: 10.1063/5.0071015.
Bandyopadhyay, et al. “ Enhanced Energy Transfer Rate in Solar Wind Turbulence Observed near the Sun from Parker Solar Probe .” The Astrophysical Journal Supplement Series, vol. 246, no. 2, 2020, p. 48, doi:10.3847/1538-4365/ab5dae.
Birn, J., and M. Hesse. “Energy Release and Transfer in Guide Field Reconnection.” Physics of Plasmas, vol. 17, no. 1, 2010, p. 12109, doi:10.1063/1.3299388.
Broeren, T., Klein, K. G. et al. “Magnetic Field Reconstruction for a Realistic Multi-Point, Multi-Scale Spacecraft Observatory.” Frontiers in Astronomy and Space Sciences, vol. 8, Sept. 2021, p. 144, doi:10.3389/fspas.2021.727076.
Chanteur, G., and C. C. Harvey. “Spatial Interpolation for Four Spacecraft: Application to Magnetic Gradients.” ISSI Scientific Reports Series, vol. 1, 1998, pp. 371–94.
Eastwood, J. P., et al. “Energy Flux Densities near the Electron Dissipation Region in Asymmetric Magnetopause Reconnection.” Physical Review Letters, vol. 125, no. 26, Dec. 2020, p. 265102, doi:10.1103/PhysRevLett.125.265102.
Fadanelli, S., B. Lavraud et al. “Energy Conversions Associated With Magnetic Reconnection.” Journal of Geophysical Research: Space Physics, vol. 126, no. 1, 2021, pp. 1–12, doi:10.1029/2020JA028333.
Guo, F., et al. “Magnetic Energy Release, Plasma Dynamics, and Particle Acceleration in Relativistic Turbulent Magnetic Reconnection.” The Astrophysical Journal, vol. 919, no. 2, IOP Publishing, 2021, p. 111, doi:10.3847/1538-4357/ac0918.
Horbury, T. S., et al. “Anisotropy in Space Plasma Turbulence: Solar Wind Observations.” Space Science Review, vol. 172, no. 1–4, Nov. 2012, pp. 325–42, doi:10.1007/s11214-011-9821-9.
Hossain, M, et al. “Phenomenology for the Decay of Energy-Containing Eddies in Homogeneous MHD Turbulence.” Physics of Fluids, vol. 7, no. 11, Nov. 1995, pp. 2886–904, doi:10.1063/1.868665.
Kármán, Th. V. “Eine Praktische Anwendung Der Analogie Zwischen Überschallströmung in Gasen Und Überkritischer Strömung in Offenen Gerinnen.” Zeitschrift Angewandte Mathematik Und Mechanik, vol. 18, no. 1, Jan. 1938, pp. 49–56, doi:10.1002/zamm.19380180108.
Kieokaew, R., et al. “Four-Spacecraft Magnetic Curvature and Vorticity Analyses on Kelvin-Helmholtz Waves in MHD Simulations.” Journal of Geophysical Research: Space Physics, vol. 123, no. 1, Jan. 2018, pp. 513–29, doi:10.1002/2017JA024424.
Klein, K. G., et al. “[Plasma 2020 Decadal] Multipoint Measurements of the Solar Wind: A Proposed Advance for Studying Magnetized Turbulence.” ArXiv E-Prints, Mar. 2019, p. arXiv:1903.05740.
Klein, K. G., et al. “Diagnosing Collisionless Energy Transfer Using Field-Particle Correlations: Alfvén-Ion Cyclotron Turbulence.” Journal of Plasma Physics, vol. 86, no. 4, Aug. 2020, p. 905860402, doi:10.1017/S0022377820000689.
Klimchuk, J. A. “On Solving the Coronal Heating Problem.”, Solar Physics, vol. 234, no. 1, Mar. 2006, pp. 41–77, doi:10.1007/s11207-006-0055-z.
Marino, R., et al. “Heating the Solar Wind by a Magnetohydrodynamic Turbulent Energy Cascade.” The Astrophysical Journal, vol. 677, no. 1, Apr. 2008, pp. L71–74, doi:10.1086/587957.
Maruca, B. A., et al. “What Are the Relative Roles of Heating and Cooling in Generating Solar Wind Temperature Anisotropies?” Physical Review Letters, vol. 107, no. 20, Nov. 2011, p. 201101, doi:10.1103/PhysRevLett.107.201101.
Maruca, B. A., et al. “MagneToRE: Mapping the 3-D Magnetic Structure of the Solar Wind Using a Large Constellation of Nanosatellites.” Frontiers in Astronomy and Space Sciences, vol. 8, July 2021, p. 108, doi:10.3389/fspas.2021.665885.
Matthaeus, W. H., et al. [Plasma 2020 Decadal] The Essential Role of Multi-Point Measurements in Turbulence Investigations: The Solar Wind beyond Single Scale and beyond the Taylor Hypothesis. no. February 2019, 2019, pp. 1–6, http://arxiv.org/abs/1903.06890.
Narita, Yasuhito, and Eckart Marsch. “Kinetic Slow Mode in the Solar Wind and Its Possible Role in Turbulence Dissipation and Ion Heating.” The Astrophysical Journal, vol. 805, no. 1, May 2015, p. 24, doi:10.1088/0004-637X/805/1/24.
Perri, Silvia, et al. “Numerical Study on the Validity of the Taylor Hypothesis in Space Plasmas.” The Astrophysical Journal Supplement Series, vol. 231, no. 1, American Astronomical Society, July 2017, p. 4, doi:10.3847/1538-4365/aa755a.
Politano, H., and A. Pouquet. “Von Kármán–Howarth Equation for Magnetohydrodynamics and Its Consequences on Third-Order Longitudinal Structure and Correlation Functions.” Physical Review E – Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, vol. 57, no. 1, 1998, pp. R21–24, doi:10.1103/PhysRevE.57.R21.
Pucci, F, et al. “Properties of Turbulence in the Reconnection Exhaust: Numerical Simulations Compared with Observations.” The Astrophysical Journal, vol. 841, no. 1, May 2017, p. 60, doi:10.3847/1538-4357/aa704f.
Pucci, F., et al. “Generation of Turbulence in Colliding Reconnection Jets.” The Astrophysical Journal, vol. 867, no. 1, Oct. 2018, p. 10, doi:10.3847/1538-4357/aadd0a.
Schwartz, S. J., et al. “Energy Conversion Within Current Sheets in the Earth’s Quasi Parallel Magnetosheath.” Geophysical Review Letters, vol. 48, no. 4, Feb. 2021, p. e91859, doi:10.1029/2020GL091859.
Shen, C, et al. “Analyses on the Geometrical Structure of Magnetic Field in the Current Sheet Based on Cluster Measurements.” Journal of Geophysical Research: Space Physics, vol. 108, no. A5, May 2003, p. 1168, doi:10.1029/2002JA009612.
Shen, C., et al. “A General Algorithm for the Linear and Quadratic Gradients of Physical Quantities Based on 10 or More Point Measurements.” Journal of Geophysical Research: Space Physics, vol. 126, no. 6, June 2021, pp. 1–19, doi:10.1029/2021JA029121.
Stawarz, J. E., J. P. Eastwood, A. Varsani, et al. “Magnetospheric Multiscale Analysis of Intense Field-Aligned Poynting Flux near the Earth’s Plasma Sheet Boundary.” Geophysical Review Letters, vol. 44, no. 14, July 2017, pp. 7106–13, doi:10.1002/2017GL073685.
Stawarz, J. E., J. P. Eastwood, T. D. Phan, et al. “Turbulence-Driven Magnetic Reconnection and the Magnetic Correlation Length: Observations from Magnetospheric Multiscale in Earth’s Magnetosheath.” Physics of Plasmas, vol. 29, no. 1, Jan. 2022, p. 12302, doi:10.1063/5.0071106.
Stawarz, J. E., et al. “Comparative Analysis of the Various Generalized Ohm’s Law Terms in Magnetosheath Turbulence as Observed by Magnetospheric Multiscale.” Journal of Geophysical Research: Space Physics, vol. 126, no. 1, 2021, pp. 1–14, doi:10.1029/2020JA028447.
Taylor, G. I. “Production and Dissipation of Vorticity in a Turbulent Fluid.” Proceedings of the Royal Society of London Series A, vol. 164, no. 916, Jan. 1938, pp. 15–23, doi:10.1098/rspa.1938.0002.
Wan, M., et al. “Von Kármán Self-Preservation Hypothesis for Magnetohydrodynamic Turbulence and Its Consequences for Universality.” Journal of Fluid Mechanics, vol. 697, Apr. 2012, pp. 296–315, doi:10.1017/jfm.2012.61.
Yang, Y., M. Wan, et al. “A Hybrid Scheme for Compressible Magnetohydrodynamic Turbulence.” Journal of Computational Physics, vol. 306, Elsevier Inc., 2016, pp. 73–91, doi:10.1016/j.jcp.2015.11.025.
Yang, Y., W. H. Matthaeus, et al. “Energy Transfer, Pressure Tensor, and Heating of Kinetic Plasma.” Physics of Plasmas, vol. 24, no. 7, 2017, doi:10.1063/1.4990421.
Yang, Y. “Energy Transfer and Dissipation in Plasma Turbulence”. Springer Singapore, 2019, doi:10.1007/978-981-13-8149-2.