Collisionless shock as a self-regulatory system – Collisionless Shock as a Self-Regulatory System

Abstract.

Collisionless shocks (CS) are one of most fundamental phenomena in
plasmas. The heliosphere is a natural laboratory for in situ studies of
these shocks but their Mach numbers are well below that of supernova
remnant (SNR) shocks. With the increase of the Mach number the shock
transition undergoes structural changes. We propose to consider this a
sequence of phase transitions. Given the upstream shock parameters, the
shock phase is determined by the ability of the corresponding structural
elements sustain stable fluxes of mass, momentum, and energy from
upstream to downstream. More than one microscopic process may lead to
the same type of CS structure. We propose an international team
consisting of specialists in heliospheric shock observations, numerical
simulations, astrophysical shocks, and theory, in order to advance this
novel paradigm.

Background.

CS are one of most fundamental phenomena in plasmas. They are
encountered in all plasma environments, from a lab to a
galaxy cluster , and at all
spatial scales, from mm to kpc. SNR shocks are one of the most efficient
accelerators of charged particle in the universe. SNR shocks are one of
the most efficient accelerators of charged particle in the
universe . The
heliosphere is the only place where CS can be studied with in situ
measurements whereas these shock Mach numbers are well below those for
SNR shocks. Understanding SNR shocks requires knowledge of CS structure
at high Mach numbers. With the increase of the Mach number, the shock
magnetic field profile undergoes structural changes from a nearly
monotonic (MT) transition to a planar stationary (PS) profile, to
rippled, reforming, and possibly turbulent states, as illustrated in
Fig. 1.

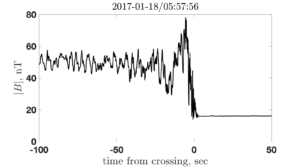
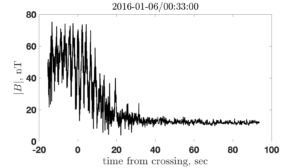
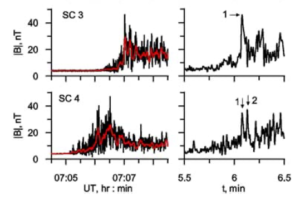
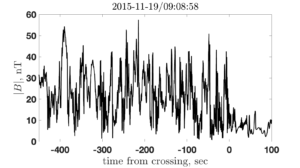
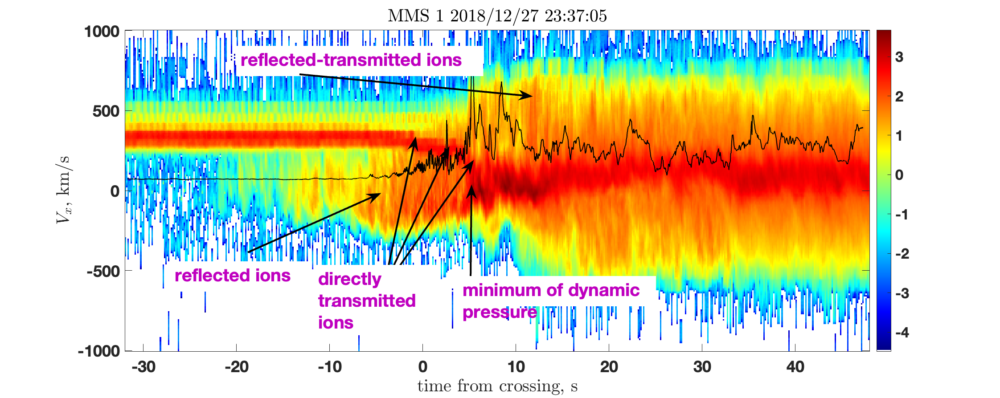
Top left: phase A – the Alfvénic Mach number $M_A\approx 5$ and the
shock angle $\theta_{Bn}\approx 64^\circ$ , the overshoot-undershoot structure, no
indications of non-planarity or time dependence. Top right: phase B –
$M_A\approx 5.5$ and
$\theta_{Bn}\approx 58^\circ$ , multiple similar oscillations of the magnetic
field are due to ripples propagating along the shock front and sweeping
across the spacecraft which passes nearly tangentially through the
shock . Bottom left:
phase C – $M_A\approx 10$ , $\theta_{Bn}\approx 80^\circ$ , the differences in the profiles measured by four
CLUSTER probes (two shown) are interpreted as reformation .
Bottom right: phase D – $M_A\approx 12$ , $\theta_{Bn}\approx 45^\circ$ , downstream magnetic oscillations persist and no
relaxation to a uniform downstream is observed – a turbulent shock ?

Understanding these structural changes is vital for understanding
physics of very high Mach number shocks and, eventually, their heating
and accelerating efficiency. Until now this issue was not investigated
systematically. Studies typically were descriptive or focused on
possible specific mechanisms of generation of particular features and/or
particular cases of rippling of reformation.

Approach.

We suggest that a CS is a self-regulatory system, at which stable
transfer of the mass, momentum, and energy, occurs from upstream to
downstream, while adding coarse grained entropy. By stable we mean that
there are no disruptions or substantial changes on average, except those
which are caused by variations of ambient conditions. In this approach
the developing shock structure is the one which ensures this transfer.
This means, that if the transfer stability is not possible without an
overshoot, an overshoot has to be formed. If it is not possible without
rippling, rippling will develop, and so on. Since ions are the main
carriers of these conserved quantities, it is ions which are responsible
for developing the structure and it is ions which have to be most
strongly affected by it. Such self-regulation has been earlier proposed
for SNR shocks, in the form of a precursor adjusted to accelerated
particles
and probably effectively reducing the Mach number relevant for the shock
transition. A shock without ion reflection is in phase MT. If ion
reflection is significant, a shock can be in one of the phases A-D, with increased complexity of the
profile. For given upstream shock parameters, the shock is in the lowest
complexity phase in which the structural elements sustain stable fluxes
of mass, momentum, and energy. With the increase of the Mach number,
when this stability is no longer possible, the shock experiences phase
transition to the phase next in complexity. These phase transitions are
not discontinuous but may be sensitive to the change of the shock
parameters and occur within a narrow parameter range. Ideally, phases
would be separated by surfaces in the three-parameter space of $M_A$ , $\theta_{Bn}$ , and $\beta$ . The latter is the
upstream thermal-to-magnetic pressure ratio. More than one microscopic
process can lead to the transition but the phases are independent of the
transition mechanism. Instead of concentrating on particular features of
shocks in each phase, we propose to focus on the question: given the
shock parameters, can we predict the phase ? Understanding the
conditions for such transitions would allow to make more reliable
conclusions about the structure of SNR shocks and the consequences of
this structure, to be compared with observations.

Methodology.

The approach dictates modus operandi: we will analyze whether certain
types of shock structures are able to ensure stable mass, momentum, and
energy transfer in a selected range of shock parameters. Specifically,
we explore the conservation laws for mass and momentum

$\frac{\partial n}{\partial t}+\frac{\partial }{\partial x_i}\left(nV_i\right)=0$

$\frac{\partial }{\partial t}\left(nmV_i\right)+\frac{\partial }{\partial x_j}\left(nmV_iV_j + p_{ij} + \frac{B^2\delta_{ij}-2B_iB_j}{8\pi}\right)=0$

and similarly for energy. Here $i,j=x,y,z$ , where $x$ is along the shock normal, and the
hydrodynamical variables are the moments of the distribution
function.

In planar stationary shocks (phase A) only dependence on $x$ survives. Note that phase A refers to
shocks with an overshoot in which ion reflection is significant. It is
known that overshoots are present even in low-Mach number shocks without
ion reflection .
This may be used as an additional signature of phase A. Rippling (phase
B) would introduce quasi-periodicity in space and time . Reformation
(phase C) would change the behavior to impulsive .
For turbulent shocks (phase D) the above relations should be modified to
account for the turbulent fields by proper averaging. The phase D may be
especially relevant for SNR shocks where observations imply large
magnetic field fluctuations. Observations will first provide the
magnetic field profile and an estimate of the basic shock parameters,
used in subsequent shock modeling, test particle analysis (TPA), and
numerical simulations. Based on the assumption about an observed shock
phase we model the shock profile and trace ions throughout. Models for
phase A ,
phase B , and phase
C have been already
proposed and tested. For phase B and higher a numerical simulation may
be first performed to [reduce the parameter space to properly choose the
parameters for TPA. The distributions, found numerically in TPA, will be
used to calculate the density, pressure tensor, and energy density.
Using the conditions of the flux constancy, we will derive the magnetic
field which is consistent with these conditions. The work will be done
by going up in complexity, starting with the transition into phase A. If
the derived magnetic field differs substantially from the initial one,
we switch to the phase B model and perform the same analysis. Upon
reaching satisfactory agreement, we come back to performing
self-consistent simulation which will provide detailed particle
distributions all across the shock. The test-particle stage is important
since it is not possible to incorporate measured fields in
self-consistent simulations. Once there is agreement between the two
stages, we will compare the fields and distributions, derived in both,
with the fields and distributions obtained in the observations. In
addition, the conservation laws will be directly checked with the
observational data. Expertise in SNR shock observations and theory is
necessary at all stages to guide the analysis and understand what is
relevant for SNR shocks.

In all cases we strive to determine the limits of the parameter range
for each phase. The proposed research will mainly focus on the
transition to phase A and from A to B. The transition B-C will be
treated in the end. Phase D has not been studied so far in the
heliospheric shocks. It will be devoted special attention in connection
with the SNR shock observations. Whenever possible, analytical treatment
will supplement the three-stage procedure (observation, test particle
analysis, simulation).

Impact.

We propose a novel approach which is expected to significantly affect
further studies of collisionless shocks by applying the reasoning,
typical for MHD and astrophysical shocks, to the shock structure. This
approach bridges over the microscopic and macroscopic features at the
scale of the shock transition, and also the heliospheric and
astrophysical shock treatment.

M. A. Balikhin, T. L. Zhang, M. Gedalin et al.. Venus
Express observes a new type of shock with pure kinematic
relaxation. Geophys. Res. Lett., 35, L01103, 2008. doi:
10.1029/2007GL032495.
M. Gedalin. Transmitted, reflected, quasi-reflected, and multiply
reflected ions in low-Mach number shocks. J. Geophys.
Res, 121, 10, 2016. doi:
10.1002/2016JA023395.
M Gedalin, W Dröge, and Y Y Kartavykh. Dynamics of high
energy ions at a structured collisionless shock front. Astrophys.
J., 825, 149, 2016. doi:
10.3847/0004-637X/825/2/149.
M. Gedalin and N. Ganushkina. Implications of weak rippling of the
shock ramp on the pattern of the electromagnetic field and ion
distributions. J. Plasma Phys., 88, 905880301, 2022. doi:
10.1017/S0022377822000356.
I. Gingell, S. J. Schwartz, D. Burgess et al.. and hybrid
simulations of surface ripples at a marginally
quasi-parallel shock. J. Geophys. Res, 77,
736, 2017. doi:
10.1002/2017JA024538.
A. Johlander, A. Vaivads, Y. V. Khotyaintsev et al.. Shock ripples
observed by the MMS spacecraft: Ion reflection and
dispersive properties. Plas. Phys. Contr. Fus., 60, 125006,
2018. doi:
10.1088/1361-6587/aae920.
V. V. Lobzin, V. V. Krasnoselskikh, J.-M. Bosqued et al..
Nonstationarity and reformation of high-Mach-number
quasiperpendicular shocks: Cluster observations.
Geophys. Res. Lett., 34, 05107, 2007. doi:
10.1029/2006GL029095.
M. Markevitch and A. Vikhlinin. Shocks and cold fronts in galaxy
clusters. Phys. Rep., 443, 1, 2007. doi:
10.1016/j.physrep.2007.01.001.
M. Miceli. Plasma heating and particle acceleration in collisionless
shocks through astrophysical observations. Plas. Phys. Contr.
Fus., 65, 034003, 2023. doi:
10.1088/1361-6587/acb082.
O. Moullard, D. Burgess, T. S. Horbury, and E. A. Lucek. Ripples
observed on the surface of the Earth’s quasi-perpendicular
bow shock. J. Geophys. Res, 111, A09113, 2006. doi:
10.1029/2005JA011594.
C. Niemann, W. Gekelman, C. G. Constantin et al.. Observation of
collisionless shocks in a large current-free laboratory plasma.
Geophys. Res. Lett., 41, 7413, 2014. doi:
10.1002/2014GL061820.
S. A. Pope, M. Gedalin, and M. A. Balikhin. The first direct
observational confirmation of kinematic collisionless
relaxation in very low Mach number shocks near the
Earth. J. Geophys. Res, 165, 3, 2019. doi:
10.1029/2018JA026223.
C. E. Rakowski, J. M. Laming, U. Hwang et al.. 1006? ApJ,
735, L21, 2011. doi:
10.1088/2041-8205/735/1/L21.
J. Vink, R. Yamazaki, E. A. Helder, and K. M. Schure. The
relation between post-shock temperature, cosmic-ray
pressure, and cosmic-ray escape for
non-relativistic shocks. Astrophys. J., 722, 1727,
2010. doi:
10.1088/0004-637X/722/2/1727.